一、概要

线性回归用于确定两种或两种以上变量间相互依赖的定量关系，只有一个自变量的情况称为一元线性回归，大于一个自变量的情况称为多元线性回归。线性回归通常用于预测分析，广泛应用在经济、医学和工业等领域。

二、详细介绍

（一）模型介绍

1.回归分析方法

(1)统计学上，用一个函数关系式将因变量随自变量变化而变化的关系呈现出来，并称其为回归方程( 对样本而言)或回归模型( 对总体而言) 。回归分析通

常包括构建回归方程、对其回归系数进行假设检验和区间估计( 即由样本去推论总体的规律，在本质上是希望得到或接近回归模型) ，最终目的是在给定自变量的新取值条件下，预测因变量的取值; 少数场合下，会给定因变量的取值，把握自变量的取值区间( 即用于控制) 。

(2)回归分析按涉及变量的多少，分为一元回归和多元回归。按照自变量和因变量之间的关系，可分为线性回归分析和非线性回归分析。

2.公式

因变量（Y）和一个或多个自变量（X）之间建立的一种回归方程。

一元回归：

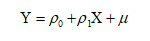
多元回归：

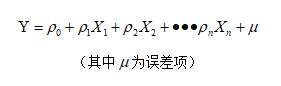
3.指标说明

R方：判定系数，用于衡量回归模型对样本观测值的拟合程度，取值范围为0-1，值越接近1，模型的拟合程度越高。

调整R方：修正自由度的判定系数，用于衡量回归模型对样本观测值的拟合程度，取值范围为0-1，值越接近1，模型的拟合程度越高。

F：F值用于判定模型中因变量与所有自变量之间的线性关系在总体上是否显著。

AIC：AIC是权衡估计模型的复杂度和模型拟合数据优良性的标准，用于模型选择，通常选择AIC最小的模型。

BIC：贝叶斯信息准则，与AIC相似，用于模型选择。

B：模型的回归系数，包括截距和斜率，显著性水平小于0.05时有意义。

标准误差：回归系数标准误差，值越大表示回归系数的估计值越不可靠。

t：对自变量进行显著性检验，以确定变量是否被保留在模型中。

Sig：显著性，如果0.01<sig<0.05为差异显著，如果sig<0.01则为差异极显著。

（二）研发依据

[1] Robinson, E. (2016). Introduction to Likelihood Statistics. Retrieved April 16, 2021 from: https://hea-www.harvard.edu/AstroStat/aas227_2016/lecture1_Robinson.pdf

[2] Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.