定义与作用:
当有两个或者两个以上的因素对因变量产生影响时,可以用多因素方差分析的方法来进行分析。多因素方差分析亦称“多向方差分析”,原理与单因素方差分析基本一致,也是利用方差比较的方法,通过假设检验的过程来判断多个因素是否对因变量产生显著性影响。在多因素方差分析中,由于影响因变量的因素有多个,其中某些因素除了自身对因变量产生影响之外,它们之间也有可能会共同对因变量产生影响。
在多因素方差分析中,把因素单独对因变量产生的影响称之为“主效应”;把因素之间共同对因变量产生的影响,或者因素某些水平同时出现时,除了主效应之外的附加影响,称之为“交互效应”。多因素方差分析不仅要考虑每个因素的主效应,往往还要考虑因素之间的交互效应。
此外,多因素方差分析往往假定因素与因变量之间的关系是线性关系。从这个方面来说,方差分析的模型也是如下一个一般化线性模型的延续:
1. 在无交互效应的情况下:因变量=因素 1 主效应+因素 2 主效应+…+因素 n 主效应+随机误差
2. 在有交互效应的情况下:因变量=因素1主效应+因素2主效应+…+因素n主效应+因素交互效应1+因素交互效应2+…+因素交互效应m+随机误差。
所以多因素方差分析往往选用一般化线性模型(General Iinear Model)进行参数估计。
基本假设:
以三因素方差分析为例:
设有三个因素A,B,C,因素A取r个水平,分别记为A1,A2,,Ar;因素B取S个水平,分别记为B1,B2,…,Bs;因素C取t个水平,分别记为C1,C2,…,Ct。在水平组合(Ai,Bj,Ck)下样本相互独立,且
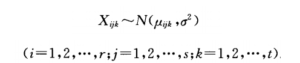
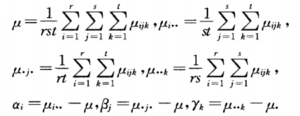
其中,i =1,2,…,r;j = 1,2,…,s;k = 1,2,…,t.称μ为一般平均,αi为因素A的第i个水平的效应,βj为因素B的第j个水平的效应,γk为因素C的第K和水平的效应。显然,αi,βj,γk满足如下关系式:
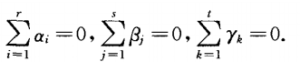
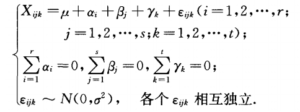
1. 提出假设
H01 : α1 = α2 = … = αr = 0,因素A对因变量没有显著影响;
H02 : β1 = β2 = … = βr = 0,因素B对因变量没有显著影响;
H03 : γ1 = γ2 = … = γr = 0,因素C对因变量没有显著影响。
2. 构造检验统计量
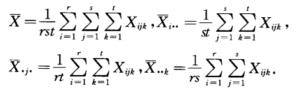
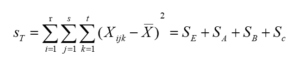
则:因素A产生的误差平方和为:
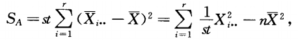
因素B产生的误差平方和为:
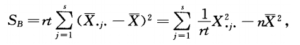
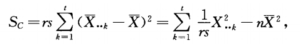
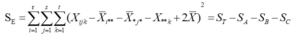

4. 检验规则
若 FA > F1-α(r-1,(r-1)(s-1)(t-1) + (r-1)(t-1) + (r-1)(s-1) + (s-1)(t- 1)),则拒绝 H01 ,表示在因素 A 的各水平下的效应有显著差异;
若 FB > F1-α(s-1,(r-1)(s-1)(t-1) + (r-1)(t-1) + (r-1)(s-1) + (s-1)(t- 1)),则拒绝 H02 ,表示在因素 B 的各水平下的效应有显著差异;
若 FC > F1-α(k-1,(r-1)(s-1)(t-1) + (r-1)(t-1) + (r-1)(s-1) + (s-1)(t- 1)),则拒绝 H03 ,表示在因素 C 的各水平下的效应有显著差异。
参考文献:
- 郭萍.三因素方差分析的原理及应用[J].沈阳大学学报(自然科学版),2015,27(1):40-43.

