一、概要
二元逻辑回归是一种对数几率模型,是离散选择法模型之一,属于多重变量分析范畴,是社会学、生物统计学、临床、数量心理学和计量经济学等统计实证分析的常用方法。
二、详细介绍
(一)模型介绍
1.逻辑回归方法
(1)逻辑回归是一种广义线性回归,因此与多重线性回归分析有很多相同之处。模型形式基本上相同,区别在于因变量不同,多重线性回归直接将wx+b作为因变量,而逻辑回归则通过函数L将wx+b对应一个隐状态p,即p=L(wx+b),然后再根据p与1-p的大小决定因变量的值。如果L是logistic函数就是逻辑回归,如果L是多项式函数就是多项式回归。
(2) 逻辑回归的因变量可以是二分类的,也可以是多分类的,但是二分类的更为常用,也更加容易解释,多类可以使用softmax方法进行处理。实际中最为常用的就是二分类的逻辑回归。
2. 公式
因变量(Y)和一个或多个变量(X)之间建立的一种回归方程。
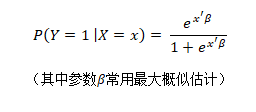
3. 指标说明
-2log likelihood:似然函数值自然对数的-2倍,反映模型的拟合程度,其值越小表示拟合程度越好。
Pseudo R方:McFadden 伪R方值,衡量回归模型对样本观测值的拟合程度,取值范围为0-1,值越接近1,模型的拟合程度越高。
AIC:AIC是权衡估计模型的复杂度和模型拟合数据优良性的标准,用于模型选择,通常选择AIC最小的模型。
BIC:贝叶斯信息准则,与AIC相似,用于模型选择。
B:模型的回归系数,包括截距和斜率,显著性水平小于0.05时有意义。
标准误差:回归系数标准误差,值越大表示回归系数的估计值越不可靠。
z: 对自变量进行显著性检验,以确定变量是否被保留在模型中。
Sig:显著性,如果0.01<sig<0.05为差异显著,如果sig<0.01则为差异极显著。
Exp(B):优势比
(二)研发依据
[1] Edge, M. (2021). Statistical Thinking from Scratch: A Primer for Scientists.
[2] Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.

