Text similarity calculation function: the platform supports MinHashLSH method currently. Aggregate modeling for the text content under preset conditions, including: screening data, selecting similarity calculation methods, similarity thresholds, etc.

1. MinHashLSH Model Introduction

(1) Jaccard index

Given sets A and B, the Jaccard coefficient is defined as the ratio of the number of elements in the intersection of A and B to the number of elements in the union of A and B, namely: J(A, B) = |A∩B| / |A∪B| = |A∩B| / (|A| + |B| – |A∩B|), used to compare the similarity and difference between finite sample sets, the larger the coefficient value, the higher the similarity. For example, A = {a,b,c,d},B = {c,d,e,f}, then the Jaccard similarity coefficient is 2/6=0.33.

(2). MinHash

MinHash is different from the traditional hash algorithm in that it no longer randomly maps the text content to the signature value, but the signature that can satisfy the similar text is also similar. The basic principle is that in the random domain of A∪B, the probability of the selected element falling in the area of ​​A∩B is equal to the Jaccard similarity, which can be used for large-scale clustering. The specific operation is to randomly arrange the n dimensions of A and B (that is, the index is randomly scrambled), and take the first non-zero index value of the vector A and B respectively as the MinHash value, then the probability P(minHash(A) = minHash(B)) = Jaccard(A,B).

(3). LSH (Locality Sensitive Hashing）

Minhash solves the operation of high-dimensional sparse vectors, but the time complexity of comparing sets pairwise is still O(n2). If the number of sets is extremely large, we hope to compare only those sets with high similarity, and ignore the collections with very low similarity. Locality-sensitive hashing (LSH) is the solution to this problem. LSH is an algorithmic technique that hashes similar input items into the same “buckets” with high probability. The basic idea is that the points in the original space are similar (similar). After being mapped by the LSH hash function, there is a high probability that the hash value is the same; and for two points that are far apart (not similar), the probability that the hash values ​​are equal after mapping is small.

2. Algorithm Description

When calculating text similarity, first obtain the document-term matrix, such as:

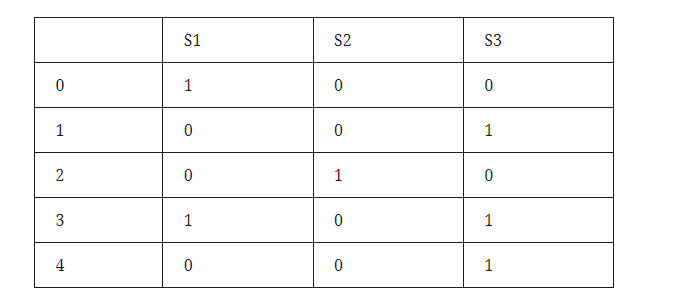
Among them, S1, S2, and S3 represent documents. The first column number 0-5 represents the row number, which is the word. In the other parts, 1 means that the document S has this word, and 0 means that the document S does not have this word. Next, use the hash function to generate the line number sequence, such as (x+1)mod5, (3x+1)mod5, then the two hash functions generate the line number sequence:

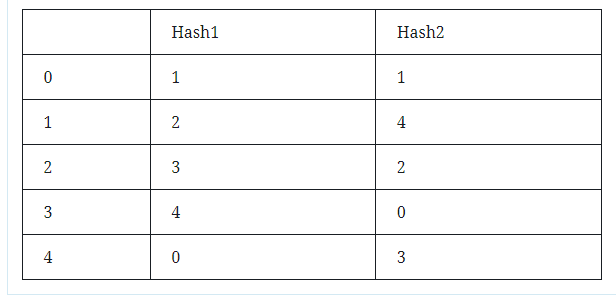
By traversing the values ​​in the matrix, skipping for 0; and for 1, check the row number generated by the hash function, find the value with the smallest row number as the value of the hash output, and finally get the following matrix:

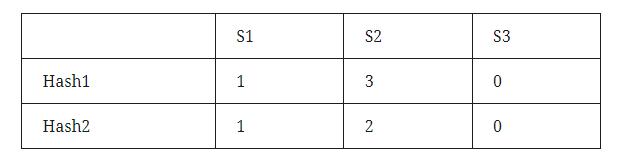
Now, the similarity of S1, S2, J(S1, S2)=0/3=0. The rationality of Minhash calculation is that the probability that the minhash value of the random row arrangement of the two sets is equal is equal to the Jaccard similarity of the two sets. For two sets A and B, there are three states for each row: (1) A and B sets have this word; (2) A and B sets do not have this word; (3) A and B sets have only one The collection has this word. If the number of rows belonging to states (1), (2), and (3) are n1, n2, and n3 in sequence, then Jaccard(A,B)=n1/(n1+n3); since the arrangement is random, then The probability of encountering (1) before encountering (3) is n1/(n1+n3), which is exactly equal to the Jaccard coefficient value.